Discrete Math - Vertex Edge Graphs
Understand and apply vertex-edge graphs.
Investigate properties of vertex-edge graphs
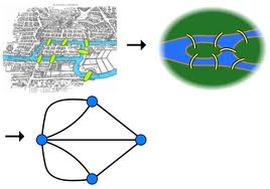
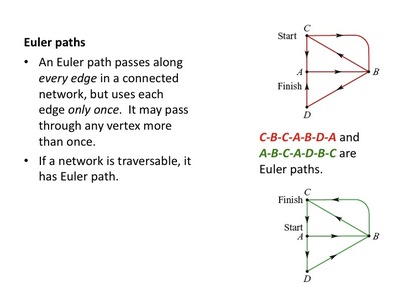
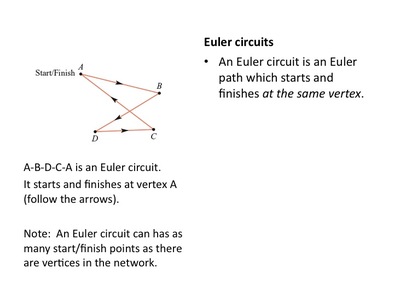
· Euler paths, · Euler circuits, and · degree of a vertex. Seven Bridges of KönigsbergThe city of Königsberg in Prussia (now Kaliningrad, Russia) was set on both sides of the Pregel River, and included two large islands which were connected to each other and the mainland by seven bridges.
The problem was to find a walk through the city that would cross each bridge once and only once. The islands could not be reached by any route other than the bridges, and every bridge must have been crossed completely every time. Euler proved that the problem has no solution. There could be no non-retracing continuous curve that passed through all seven of the bridges. |
Draw This - one continuous motion
Doug Ensley
Leadership Program: Exploring Discrete Mathematics in the Classroom
Discrete Math by Mrs. Morey
Learner - Mathematics Illuminated - Euler
..................... Thursday, January 19th .....................
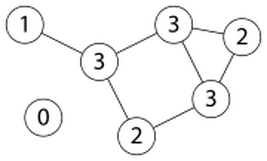
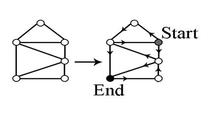
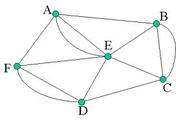
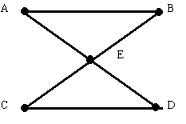
Warm-up: Have you come up with any rule that would allow you to know if a graph is traceable or not without having to trace the figure? Look at a design of the board and discuss the number of odd and even vertices.
LOOK FOR A PATTERN
Lesson:
Look at the patterns in the data that was collected yesterday.
Discover 3 rules.
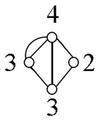
Rule 1: If there are 2 odd vertices. the graph is traceable. You start at one odd vertice and end at the other one.
Rule 2: If there are more than 2 odd vertices the graph is not traceable.
Rule 3: If there are all even vertices the graph is traceable and you can start anywhere and will end at the place you started.
Homework:
Draw a map of a made up city (be creative) using vertices and edges. Ask a question relating to the start and endpoint, is it traceable, or where do you need to draw a road to make it traceable.
LOOK FOR A PATTERN
Lesson:
Look at the patterns in the data that was collected yesterday.
Discover 3 rules.
Rule 1: If there are 2 odd vertices. the graph is traceable. You start at one odd vertice and end at the other one.
Rule 2: If there are more than 2 odd vertices the graph is not traceable.
Rule 3: If there are all even vertices the graph is traceable and you can start anywhere and will end at the place you started.
Homework:
Draw a map of a made up city (be creative) using vertices and edges. Ask a question relating to the start and endpoint, is it traceable, or where do you need to draw a road to make it traceable.